In the realm of nonlinear dynamic systems, a small change in one area can have significant consequences elsewhere. Examples of such systems include climate patterns, the intricate workings of the human brain, and the behavior of the electric grid. These systems undergo profound transformations over time, making them exceedingly challenging to model accurately. However, in recent years, researchers have turned to a machine-learning technique called reservoir computing, which has shown promise in modeling high-dimensional chaotic behaviors with relative simplicity. Yuanzhao Zhang, a Complexity Postdoctoral Fellow at SFI, acknowledges the growing trend of using machine learning to learn complex dynamic systems with limited mathematical understanding. In particular, reservoir computing has shown the ability to predict the trajectory of chaotic systems with minimal training data and to determine the system’s future states from its initial conditions. This exciting prospect led Zhang to investigate the truth behind these claims and uncover any overlooked limitations in reservoir computing’s effectiveness.
In a collaboration with physicist Sean Cornelius from Toronto Metropolitan University, Zhang conducted a comprehensive analysis of reservoir computing and its newer variant known as next-generation reservoir computing (NGRC). Their findings, published in Physical Review Research, shed light on the limitations of these techniques that have been largely overlooked by the research community. Zhang describes one of these limitations as a “Catch-22” scenario, highlighting its intractability, particularly for complex dynamic systems. Reservoir computing, first proposed by computer scientists over two decades ago, employs neural networks to build a predictive model that is simpler and more cost-effective to train compared to other neural net frameworks. The NGRC variation offers additional advantages, including the ability to train with less data. While recent studies have demonstrated the potential power of RC and NGRC in modeling dynamic systems, Zhang and Cornelius discovered deficiencies in these approaches under certain conditions.
The Catch-22 Problem in NGRC
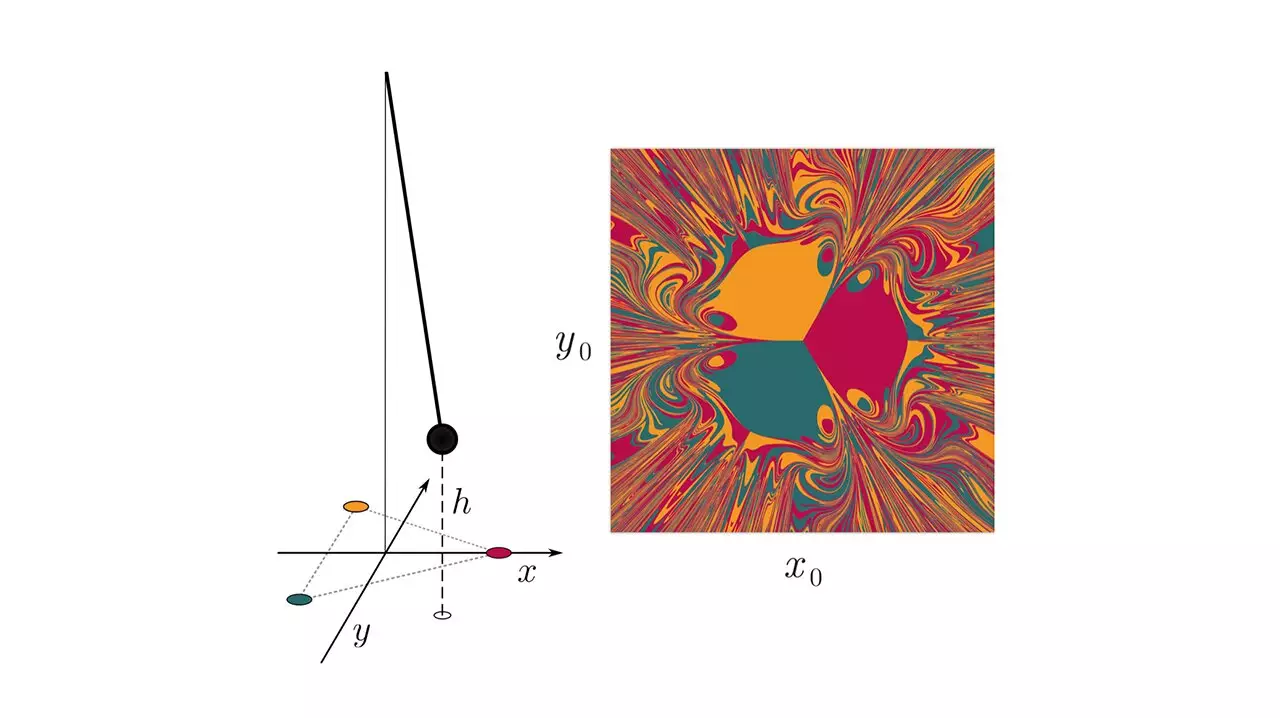
To surface the limitations of NGRC, Zhang and Cornelius investigated a straightforward dynamic chaotic system: a pendulum with a magnet attached, swinging among three fixed magnets positioned in a triangular formation. Their experiments revealed that when information about the specific nonlinearity required to describe the system was provided, NGRC performed admirably. “In a sense, you have this kind of information sneaked in before the training begins,” explains Zhang. However, when the model was perturbed or subjected to disturbances, its performance significantly deteriorated. This indicates that NGRC struggles to make accurate predictions unless crucial information about the system being modeled is explicitly incorporated into the training phase. The researchers’ findings emphasize the necessity of considering how NGRC can handle disturbances and unpredictable events, which are common in real-world scenarios.
The Warm-Up Time Challenge in RC
In their examination of RC, Zhang and Cornelius observed another limitation relating to the model’s “warm-up” time. Before correctly predicting the system’s behavior, the RC model requires an extended warm-up period that is nearly as time-consuming as the actual dynamic movements of the magnet. This signifies an additional obstacle in applying RC effectively, as the warm-up time can become impractical for real-time predictions or situations demanding immediate responses. Addressing these limitations in both RC and NGRC holds significant potential for researchers to leverage the full capabilities of this emerging computing framework.
Understanding the limitations of reservoir computing is crucial for researchers seeking to harness its potential in modeling complex dynamic systems. By acknowledging the challenges presented by the Catch-22 problems in NGRC and the warm-up time in RC, scientists can explore strategies to overcome these obstacles. Developing techniques that enable NGRC to handle disturbances and perturbations more effectively will enhance its predictive capabilities in real-world scenarios. Similarly, finding ways to reduce or optimize the warm-up time in RC models can improve their usability and applicability in time-sensitive situations. The ongoing exploration and refinement of reservoir computing will provide valuable insights into its capabilities and limitations, ultimately paving the way for more accurate and reliable predictions in the realm of nonlinear dynamic systems.
As computational power continues to advance and research efforts expand, reservoir computing holds significant promise in revolutionizing our understanding of complex dynamic systems. By integrating machine learning techniques with mathematical modeling, researchers can uncover hidden patterns and dependencies that were previously elusive. However, a critical awareness of the limitations is essential to harness reservoir computing’s true potential effectively. As scientists continue to deepen their understanding of these limitations and develop innovative solutions, reservoir computing will undoubtedly play a pivotal role in advancing our understanding of nonlinear dynamic systems, making it an invaluable tool for various scientific and practical applications.

Leave a Reply